Numbers are fundamental building blocks in mathematics, used for counting, measuring, and performing various operations. They hold specific characteristics and follow certain rules when performing mathematical operations. Their properties apply to specific operations like addition, multiplication, subtraction, and division. Understanding these properties makes performing calculations easier and helps develop a deeper understanding of mathematical concepts. In this blog, we will explore the fundamentals of even numbers and discuss their properties and patterns.
What are Even numbers?
Mathematically, an even number can be defined as an integer n that is divisible by 2:
n / 2 = an integer (with no remainder) In simple words, even numbers are integers that can be exactly divided by 2. They always end with the last digit as 0, 2, 4, 6, or 8.
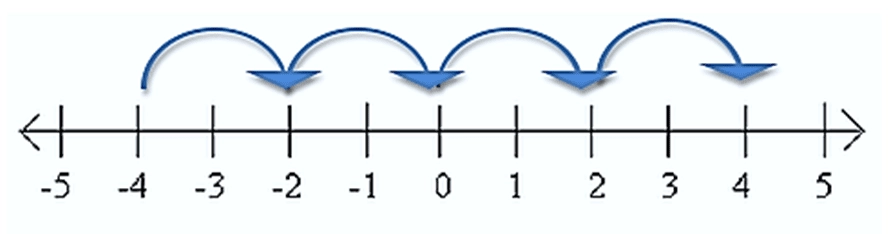
Some examples of even numbers are: 2, 4, 6, 8, 10, 12, 14 and so on. Any number that ends in 0, 2, 4, 6, or 8 is an even number. This includes negative even numbers such as -2, -4, -6 and so on.
General Form of Even Numbers An even number can be expressed using the following formula:
[ N = 2k ] Where:
(N) represents the even number.
(k) represents any whole number (an integer).
In this general form, we multiply 2 by any whole number (k) to obtain an even number (N). Example: If we replace (k) with 6, we get: [ N = 2 x 6 = 12 ] So, (12) is an even number.
Is zero an even number? Yes, zero is considered an even number. An even number is defined as an integer that is divisible by 2, meaning it leaves no remainder when divided by 2. Zero fits this definition because when you divide zero by 2, the result is zero with no remainder. Additionally, zero shares many characteristics with other even numbers, including negative numbers and the property of subtraction. Example: Zero can be represented as 2 × 0, indicating that it is indeed a multiple of 2. Also, like other even numbers, when you add or subtract zero to or from another even number, the result remains even.
0 = 2 × 0
So the number 0 can be expressed as 2k where k = 0. So, in summary, zero is an even number because it is divisible by 2 and exhibits properties similar to other even numbers.
Properties of Even Numbers 1) Addition Property
Even number + Odd number = Odd number.
Even number + Even number = Even number.
Odd number + Odd number = Even number.
2) Subtraction Property: This property of subtraction states that when subtracting an even number from another even number, the difference will always be an even number. For example, 16 - 10 = 6. This also applies to subtracting an even number from an odd number or an odd number from an even number, where the difference will always be an odd number.
Even number - Odd number = Odd number.
Even number - Even number = Even number.
Odd number - Odd number = Even number.
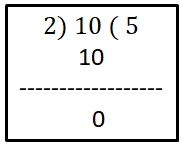
3) An even number is divisible by 2 with no remainder. spell-check needed in the image below
10 ÷ 2 = 5 (No remainder)
4) The product of two even numbers will be even. Example:
2 × 2 = 4
4 × 4 = 16
6 × 6 = 36 5) The difference between two even numbers will be even. Example:
6 - 2 =4
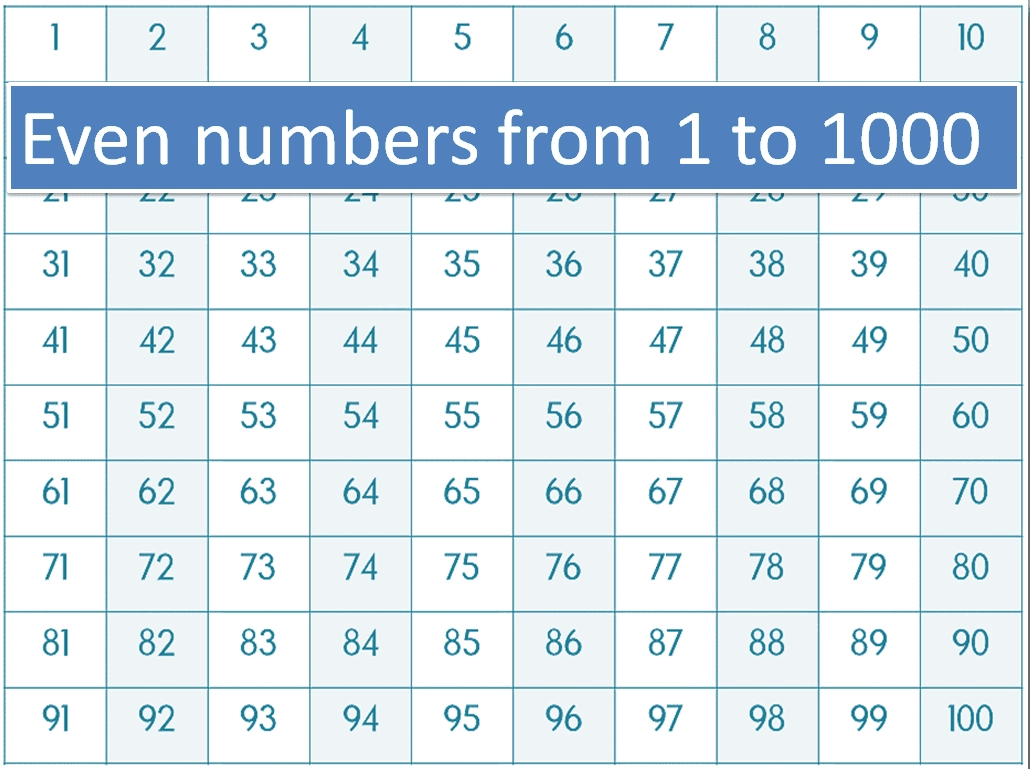
8 - 4 = 4 6) In the decimal system, even numbers always end in 0, 2, 4, 6, or 8. Example: 24, 86, 98, and 102 are all even numbers in the decimal system and they end with even digits. 7) There are 500 even numbers between 1 and 1000. 8) Even numbers, with a total of 500 in the range of 1 to 1000, have a special property when added together. This is known as the sum of even numbers formula, S = n(n+1), where n is the total number of even numbers, which in this case is 500. This formula can be used to calculate the sum of all even numbers from 1 to 1000, which is 250,500.
Characteristics of Even Numbers
All even numbers are integers, meaning they have no fractional or decimal part.
Even numbers represent quantities that can be divided equally into two groups, highlighting their divisibility by 2. In other words, the numbers can be grouped into pairs or equal groups of 2, making them even.
Even numbers often exhibit a sense of symmetry since they can be split into two identical halves.
Even numbers alternate with odd numbers in the sequence of natural numbers. So even numbers appear after every odd number. (odd, even, odd, even, and so on).
Looking for math instructor? Hire EnthuZiastic Math Experts to master in math no time.
Do you Know? Some of the most significant applications and uses of even numbers include:
Counting and measuring objects in pairs - this includes counting physical objects like shoes that come in pairs. Even numbers are useful for pairing.
Indexing pages in books and documents. Page numbers are usually even to allow facing pages to be odd and even.
Numbering houses on streets, rooms in hotels and several other real-world objects.
Even and odd parity bits are used in error detection in data transmission and storage.
Most computer memory addresses are even numbers as data is stored in words of even byte lengths.
Spreading workload evenly across processors in parallel and distributed computing. Even dispersion helps optimize computing
In ancient China, even numbers were associated with Yin, the feminine and passive principle, while odd numbers represented Yang, the masculine and active principle.
In numerology, even numbers are often associated with balance, harmony, and peace.
List of Even Numbers from 0 to 500
List of Even Numbers from 501 to 1000
FAQs
1. What is the mathematical definition of an even number? An even number is defined mathematically as an integer n that is divisible by 2 with no remainder. 2. Name two characteristics of even numbers. Two characteristics of even numbers are: 1) They are exactly divisible by 2, and 2) They alternate with odd numbers in the sequence of natural numbers. 3. Give three examples of even numbers less than 20. Three examples of even numbers less than 20 are: .Give any 3 only as the question says so. you may mention any 3 from this set. 4. What is one real-world application where even numbers play a significant role? One real-world application is numbering houses on streets or rooms in hotels. Even and odd numbers are used alternately for orderly numbering and spacing. 5. What is the smallest even number? Is it not 0? 6. Is zero an even number? Yes, zero is an even number because it is divisible by 2. 7. If you subtract an even number from another even number, what type of number do you always get? When you subtract an even number from another even number, you always get an even number as a result. 8. What is the sum of the first five even numbers? The sum of the first five even numbers is 2 + 4 + 6 + 8 + 10 =30. The formula to sum the first n even numbers is:
n × (n + 1)
=5 × (5+1)
=5 × 6
=30
