Odd Numbers From 1 to 1000 

“Mathematics is an universal language. And numbers are its soul.”

Numbers show various properties according to situations. They range from prime numbers to rational numbers. These categories provide a framework for understanding the diverse properties and characteristics of numbers in mathematics. Similarly, odd and even numbers play a surprisingly important role in both mathematics and the real world, though their importance varies depending on the context. Even numbers are integers that are divisible by 2, while odd numbers are integers that are not divisible by 2 and can be represented on a number line. Understanding the concept of odd numbers is essential in developing a strong foundation in mathematics.

While odd and even numbers might seem simple, their impact extends far beyond basic counting. They are fundamental tools in mathematics, play a role in countless real-world applications, and even hold cultural and symbolic significance in some societies.

In this blog, we will explore the importance of odd numbers and the fundamentals of their properties.

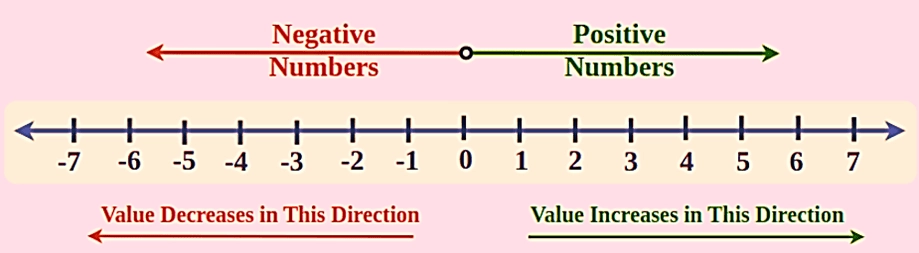
Odd Numbers

Odd numbers are a subset of integers that cannot be divided evenly by 2. In other words, when an odd number is divided by 2, it does not result in a whole number. Instead, there is always a remainder of 1.

Examples: Odd numbers include 1, 3, 5, 7, 9, and 11.

Identifying Odd Numbers

The best way to spot an odd number is to divide it by 2. If the number does not divide evenly, leaving a remainder of 1, then it is an odd number.

Example:

5/2 = 2 with remainder 1.

7/2 = 3 with remainder 1.

So 5 and 7 are odd numbers.

On the flip side, even numbers can be divided by 2 evenly without leaving any remainder.

Example:

6 / 2 = 3

and

8 / 2 = 4

No remainder!

This is why even numbers end in 0, 2, 4, 6 or 8.

Why are Odd Numbers important to learn?

Introducing the concept of even numbers to children after they have a grasp on odd numbers can further enhance their understanding and application of numbers in mathematics. Additionally, it is important to note the significance of composite odd numbers, such as 15 and 21, which are formed by multiplying two smaller positive integers or multiplying the number with one.

These numbers may seem simple, but they play a crucial role in understanding the properties of numbers and their relationships in mathematics. In fact, understanding composite odd numbers such as 15 and 21, which are formed by adding 2 to the previous odd number, can help in identifying patterns and solving problems in various mathematical concepts, especially in consecutive odd numbers.

Solved examples of odd numbers, such as 3 + 5 = 8 and 7 + 3 = 10, can further illustrate the concept of addition of odd numbers and their resulting even numbers. Additionally, understanding odd composite numbers, such as 15 and 21, which have more than two factors or are not prime, can provide a deeper understanding of the properties of numbers.

Significance of the Odd Numbers

Beyond their mathematical definition, odd numbers hold a curious significance across various fields. In mathematics, they hold the key to countless theorems and properties, while in numerology, they symbolize individuality, creativity, and dynamism.

Historically, odd numbers have been imbued with spiritual meaning in various cultures, often representing completion or good luck. Even in everyday life, we see their influence: from the three wishes in a fairy tale to the single, burning candle symbolizing hope.

While seemingly simple, odd numbers weave a fascinating tapestry of meaning, reminding us that even the smallest difference can hold profound significance.

A chart of odd numbers from 1 to 100

1	3	5	7	9
11	13	15	17	19
21	23	25	27	29
31	33	35	37	39
41	43	45	47	49
51	53	55	57	59
61	63	65	67	69
71	73	75	77	79
81	83	85	87	89
91	93	95	97	99

Properties of odd numbers 

• Divisibility: An odd number cannot be evenly divided by 2. In other words, dividing an odd number by 2 will result in a quotient that is not an integer (there will be a remainder of 1).

9 ÷ 2 =4 ( Remainder 1)

11 ÷ 2 = 5 ( Remainder 1)

• Representation: Odd numbers are commonly represented as 2k+1, where k is an integer. This representation ensures that when you multiply an odd number by 2 and add 1, you get another odd number. It’s very similar to the general form of an even number which is n=2k.

{2k + 1 | k ∈ Z}

n=2k+1

• This means the set of all odd numbers is the collection of all numbers that can be written as the expression 2k + 1, where k is any integer (Z).
• The number n is an odd number if it can be expressed as 2k+1 where k is just another integer.

Example:

7 → 7 = 2 ( 3 ) + 1

23 → 23 = 2 ( 11 ) + 1

49 → 49 = 2 ( 24 ) + 1

• Addition and Subtraction: The sum or difference of two odd numbers is always an even number.

Example:

3+5=8

9−5=4

• Multiplication: The product of two odd numbers is always odd.

Example:

3 × 5 =15

7 × 9 = 63

• Division: When an odd number is divided by another odd number, the result can be either odd or fractional.

Example:

9 ÷ 3 = 3 (odd)

15 ÷ 5 = 3 (odd)

Operation	Result
Odd + Odd	Even
Odd – Odd	Even
Odd × Odd	Odd
Odd ÷ Odd	Odd

• The squares of odd numbers like 1, 9, 25, 49, 81, 121 etc. are again odd numbers. This pattern continues for higher odd number squares too.
• The formula for the sum of the first n odd numbers is: Sum=n2

Interesting Facts

• Ancient Greeks considered odd numbers to be masculine and even numbers to be feminine.
• 99 is the greatest two-digit odd number.
• There are a total of 50 odd numbers between 1 to 100.
• The sum of first 500 odd numbers equals 250,000.
• The sum of all the odd numbers from 1 to 100 is 2500.
• The average or mean of all odd numbers between 1 to 100 is 50.
• Odd numbers have an abundance of primes. More than half of all prime numbers are odd numbers.
• Many prime numbers are odd. Prime numbers are those greater than 1 with no positive divisors other than 1 and themselves. Examples include 3, 5, 7, 11, and so forth.
• There are infinitely many odd numbers. You can always find another odd number by adding 2 to the previous one.

Odd Numbers from 101 to 200

101	111	121	131	141	151	161	171	181	191
103	113	123	133	143	153	163	173	183	193
105	115	125	135	145	155	165	175	185	195
107	117	127	137	147	157	167	177	187	197
109	119	129	139	149	159	169	179	189	199

Odd Numbers from 201 to 300

201	211	221	231	241	251	261	271	281	291
203	213	223	233	243	253	263	273	283	293
205	215	225	235	245	255	265	275	285	295
207	217	227	237	247	257	267	277	287	297
209	219	229	239	249	259	269	279	289	299

Odd Numbers from 301 to 400

301	311	321	331	341	351	351	361	371	381
303	313	323	333	343	353	353	363	373	383
305	315	325	335	345	355	355	365	375	385
307	317	327	337	347	357	357	367	377	387
309	319	329	339	349	359	359	369	379	389

Odd Numbers from 401 to 500

401	411	421	431	441	451	461	471	481	491
403	413	423	433	443	453	463	473	483	493
405	415	425	435	445	455	465	475	485	495
407	417	427	437	447	457	467	477	487	497
409	419	429	439	449	459	469	479	489	499

Odd Numbers from 501 to 600

501	511	521	531	541	551	561	571	581	591
503	513	523	533	543	553	563	573	583	593
505	515	525	535	545	555	565	575	585	595
507	517	527	537	547	557	567	577	587	597
509	519	529	539	549	559	569	579	589	599

Odd Numbers from 601 to 700

601	611	621	631	641	651	661	671	681	691
603	613	623	633	643	653	663	673	683	693
605	615	625	635	645	655	665	675	685	695
607	617	627	637	647	657	667	677	687	697
609	619	629	639	649	659	669	679	689	699

Odd Numbers from 701 to 800

701	711	721	731	741	751	761	771	781	791
703	713	723	733	743	753	763	773	783	793
705	715	725	735	745	755	765	775	785	795
707	717	727	737	747	757	767	777	787	797
709	719	729	739	749	759	769	779	789	799

Odd Numbers from 801 to 900

801	811	821	831	841	851	861	871	881	891
803	813	823	833	843	853	863	873	883	893
805	815	825	835	845	855	865	875	885	895
807	817	827	837	847	857	867	877	887	897
809	819	829	839	849	859	869	879	889	899

Odd Numbers from 901 to 1000

901	911	921	931	941	951	961	971	981	991
903	913	923	933	943	953	963	973	983	993
905	915	925	935	945	955	965	975	985	995
907	917	927	937	947	957	967	977	987	997
909	919	929	939	949	959	969	979	989	999

FAQs

1) What is the defining characteristic of odd numbers?

Odd numbers are integers that cannot be divided evenly by 2, leaving a remainder of 1 when divided by 2.

2) How many odd numbers are there from 1 to 1000?

There are 500 odd numbers from 1 to 1000. Odd numbers are integers that cannot be divided evenly by 2 and have a remainder of 1 when divided by 2. In this range, every other number is odd, so there are 500 odd numbers in total.

3) What is the largest odd number between 1 and 1000?

The largest odd number between 1 and 1000 is 999. Odd numbers are numbers that cannot be divided evenly by 2, leaving a remainder of 1 when divided by 2. Since 1000 is an even number, the largest odd number in this range would be 999.

4) Can an odd number be both a perfect square and a prime number? If so, can you provide an example?

No, an odd number cannot be both a perfect square and a prime number.

Here’s why:

• A perfect square is an integer which can be expressed as the product of two identical integers. For example, 4 is a perfect square because 4 = 2 x 2.

• An odd number, by definition, is not divisible by 2. This means that when you prime factorize an odd number, you won’t have 2 (or any even number) as a factor.

Since a perfect square requires multiplying two identical integers, and one of those integers must always be even (2), it follows that an odd number cannot be a perfect square. Therefore, an odd number cannot be both a perfect square and a prime number.

5) What property of odd numbers states that their addition always results in an even number?

When you add two odd numbers together, the result is always an even number.

Example: 5 + 5 = 10

6) How can you identify odd numbers from 1 to 1000 using the modulo operator?

You can use the modulo operator (%). If a number divided by 2 leaves a remainder of 1, then it’s an odd number.

Example: 7 % 2 equals 1 because 7 divided by 2 leaves a remainder of 1.

7) If you subtract 1 from any odd number, what type of number will you get?

If you subtract 1 from any odd number, you will get an even number.

Example: 5 – 1 = 4

8) If you multiply two odd numbers together, do you always get an even or odd number?

An odd number. The product of any two odd numbers will always be odd because any odd number multiplied by 1 (which is technically multiplying by itself) will remain odd.

Conclusion

Odd numbers, standing apart from their even counterparts, hold intrigue beyond just their mathematical definition. In mathematics, they form the building blocks of primes, the essential ingredients of number theory. They possess unique properties and exhibit interesting patterns. From identifying them using simple methods to understanding their significance in various mathematical concepts, odd numbers never cease to intrigue us.