A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, a prime number is a whole number greater than 1 that cannot be formed by multiplying two smaller natural numbers. In this enthusiastic blog, let's explore the prime numbers from 1 to 100, unraveling their secrets and exploring their significance.
What Are Prime Numbers?
Definition: A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself. In other words, prime numbers cannot be divided evenly by any other numbers except 1 and the number itself. Examples: 2, 3, 5, 7, 11, 13, 17, 19, etc. Illustration: Imagine a rectangular cake. You can only cut it perfectly into even pieces (with no remainders) if the number of pieces matches the length or width of the cake (which is itself a factor), or if you cut it into 1 piece (itself). Prime numbers, like indivisible cakes, only have these two cutting options. Example: 2, 3, 5, and 7 are all prime numbers. Here's why:
2 can only be divided by 1 and 2.
3 can only be divided by 1 and 3.
5 can only be divided by 1 and 5.
7 can only be divided by 1 and 7.
On the other hand, numbers like 4, 6, and 9 are not prime. They can be factored into a product of smaller natural numbers: ⇒ 4 (2 x 2) ⇒ 6 (2 x 3) ⇒ 9 (3 x 3)
2, 3, 5, 7, and 11 are prime numbers because they cannot be divided by any other number except 1 and the number itself.
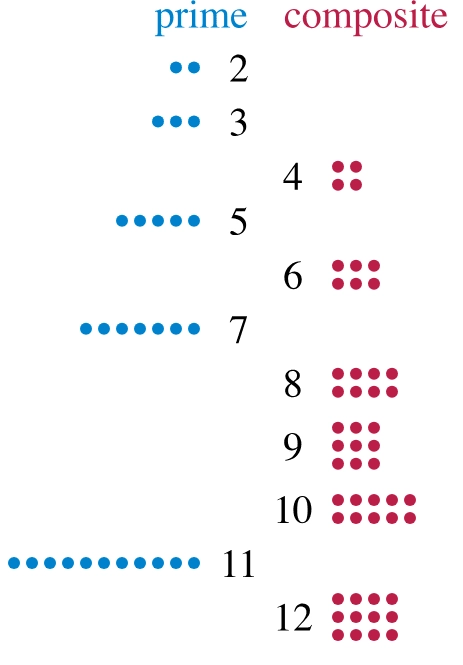
The non-prime numbers are called composite numbers. Fun Fact: Did you know that prime numbers are sometimes called "lonely numbers" because they have no other divisors apart from 1 and themselves?
Properties of Prime Numbers Here are some key properties of prime numbers:
Prime numbers have exactly two distinct divisors: 1 and the number itself.
The number 1 is not considered prime by modern definitions.
Prime numbers are infinitely many (never ending).
Every number greater than 1 is either prime or can be expressed as a unique product of prime factors.
List of Prime Numbers from 1 to 100 The prime numbers from 1 to 100 are:
2 | 13 | 31 | 53 | 73 |
3 | 17 | 37 | 59 | 79 |
5 | 19 | 41 | 61 | 83 |
7 | 23 | 43 | 67 | 89 |
11 | 29 | 47 | 71 | 97 |
What is a Mersenne prime? A Mersenne prime is a special type of prime number with a specific form. It's named after Marin Mersenne, a French mathematician who studied them in the 17th century.
A Mersenne prime is a prime number that can be written as 2^n - 1, where n is a whole number greater than or equal to 2.
In other words, it's a prime number that's one less than a power of 2. Here are some examples of Mersenne primes:
3 = 2^2 - 1 (2 to the power of 2 minus 1)
7 = 2^3 - 1 (2 to the power of 3 minus 1)
31 = 2^5 - 1 (2 to the power of 5 minus 1)
127 = 2^7 - 1 (2 to the power of 7 minus 1)
Not all numbers following this form are prime numbers. For instance, 2^4 - 1 (15) is not prime because it can be factored as 3 x 5. Mersenne primes are interesting because they are connected to perfect numbers, another fascinating concept in number theory. However, finding Mersenne primes gets challenging as the value of n increases, making them computationally expensive to identify.
Why are Prime Numbers Important? Prime numbers are the building blocks of natural numbers. They are significant in various fields, including: ♦ Mathematics: Prime numbers are fundamental in number theory, a branch of mathematics that studies the properties of integers. The Fundamental Theorem of Arithmetic states that every natural number greater than 1 can be uniquely factored into a product of prime numbers. This property is crucial in solving many problems in number theory and other areas of mathematics. ♦ Cryptography: Prime numbers play a vital role in modern cryptography, which is the science of secure communication. The intricacy of factoring big prime numbers is the foundation of encryption methods. ♦ Because factoring large numbers is computationally expensive, it makes it challenging to break the encryption and steal the information.
♦ Computer Science: Prime numbers have applications in various computer science areas, such as hash tables. Hash tables are data structures that efficiently store and retrieve information. They use prime numbers to minimize collisions, which occur when different data items map to the same location in the table.
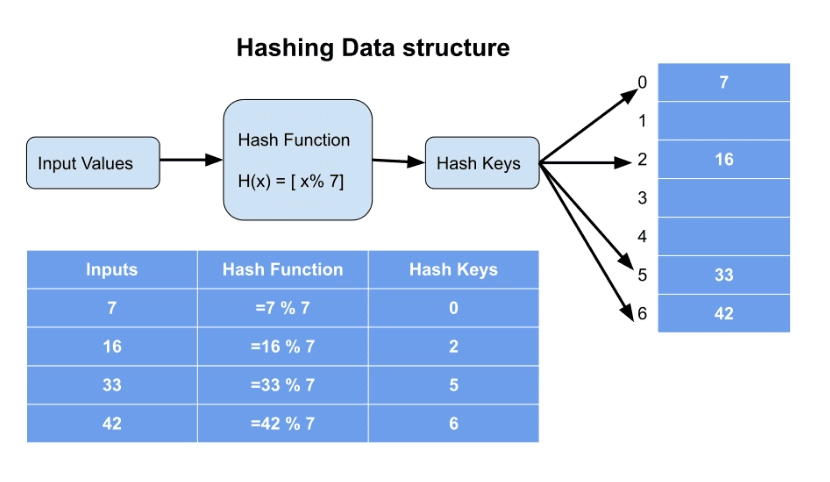
♦ Prime numbers have applications in areas like hash functions, pseudo-random number generators, and primality testing. ♦ Prime numbers are also related to unsolved problems in mathematics, such as the Riemann Hypothesis and the distribution of prime numbers. From banking transactions to internet security, prime numbers are integral to modern technology and everyday life.
Important Concepts Related to Prime Numbers Here are a few important concepts related to prime numbers, with examples:
Prime Factorization Every number greater than 1 can be expressed as a unique product of prime factors. This process is known as the factorization method, and can be applied to any number to determine its prime factorization, and the number of factors it has can be determined by counting the number of prime factors. Additionally, co-prime numbers can also be determined by finding the highest common factor (HCF) between two numbers, which is the largest number that can divide both numbers evenly. For example, the HCF of 5 and 9 is 1, making them co-prime numbers. Understanding the concept of HCF is crucial in mastering prime numbers and their properties. Example: The prime factorization of 12 is 2 x 2 x 3. This means that 12 can be broken down into the product of two 2s and a 3. We can further break down 12 by repeatedly dividing by the smallest prime number that divides it. In this case, we can continue to divide by 2 until we are left with 3, a prime number. Here are some other examples of prime factorization:
The prime factorization of 30 is 2 x 3 x 5.
The prime factorization of 60 is 2 x 2 x 3 x 5.
The prime factorization of 100 is 2 x 2 x 5 x 5.
The prime factorization of 24 is 2 x 2 x 2 x 3.
Primality Testing Determining whether a given number is prime or not. Example: The number 37 is prime because it is not divisible by any number other than 1 and itself.
Twin Primes A pair of prime numbers that differ by 2. Example:
3 and 5 are twin primes. There are infinitely many twin primes, but their pattern is not yet fully understood.
Looking for math instructor? Hire EnthuZiastic Math Experts to master in math no time.
Interesting Facts about Prime Numbers ⇔The largest known prime number, as of December 2022, is a number with 24.8 million digits, discovered by the Great Internet Mersenne Prime Search (GIMPS) project. ⇔The first 25 prime numbers were known to ancient Greek mathematicians as early as 300 BC. ⇔There is no largest prime number or smallest prime number. Prime numbers continue infinitely in both directions. ⇔Prime numbers seem to be randomly distributed among the integers, but there are many unanswered questions about their patterns and distribution.
FAQs 1. What is the definition of a prime number? A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. 2. What is the smallest prime number? The smallest prime number is 2. 3. How many prime numbers are there between 1 and 20? There are 8 prime numbers between 1 and 20: 2, 3, 5, 7, 11, 13, 17, and 19. 4. What is the sum of the first five prime numbers? The sum of the first five prime numbers is 2 + 3 + 5 + 7 + 11 = 28. 5. What is the only even prime number? 2 is the only even prime number; all other even numbers greater than 2 are divisible by 2 and therefore not prime. 6. How many prime numbers are there between 1 and 100? There are 25 prime numbers between 1 and 100, including 2 and the odd prime numbers 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97. Prime numbers are positive integers that are greater than 1 and have no divisors other than 1 and themselves, making them essential for mastering the concept of positive integers. 7. What is the largest prime number between 1 and 100? The largest prime number between 1 and 100 is 97. Prime numbers are those that are only divisible by 1 and themselves, and 97 fits this criterion as it has no other factors aside from 1 and 97.
