Geometric shapes are fundamental to our understanding of the world around us, and one such intriguing shape is the cone. Cones are visually appealing and play a significant role in various scientific and mathematical concepts.
This blog discovers the secrets to calculating the volume of a cone with ease. Our guide covers everything you need to know about finding the volume of a cone.
- Defining the Cone: A Pointy Gemstone
- 1. The key features that define a cone
- 2. Types of the cone There are two types of cones
- 3. Right Circular Cone
- 4. Oblique Cone
- 5. Significance of Cones
- 6. Calculating the Volume of a Cone
- 7. where
- 8. Breaking Down the Formula
- 9. How do you find the height of a cone given its volume and radius?
- 10. Examples and Explanations
- 11. where
- Fun Facts About Cones
- Conclusion
- FAQ’s
- 1. What is the formula for calculating the volume of a cone, and what do the variables represent?
- 2. In which areas of science are cones commonly used, and how do they play a role in those fields?
- 3. Provide an example of calculating the volume of a cone with specific values for radius and height.
- 4. How do cones contribute to our understanding of geometry and calculus in mathematics?
- 5. How does the radius and height of a cone affect its volume?
Defining the Cone: A Pointy Gemstone
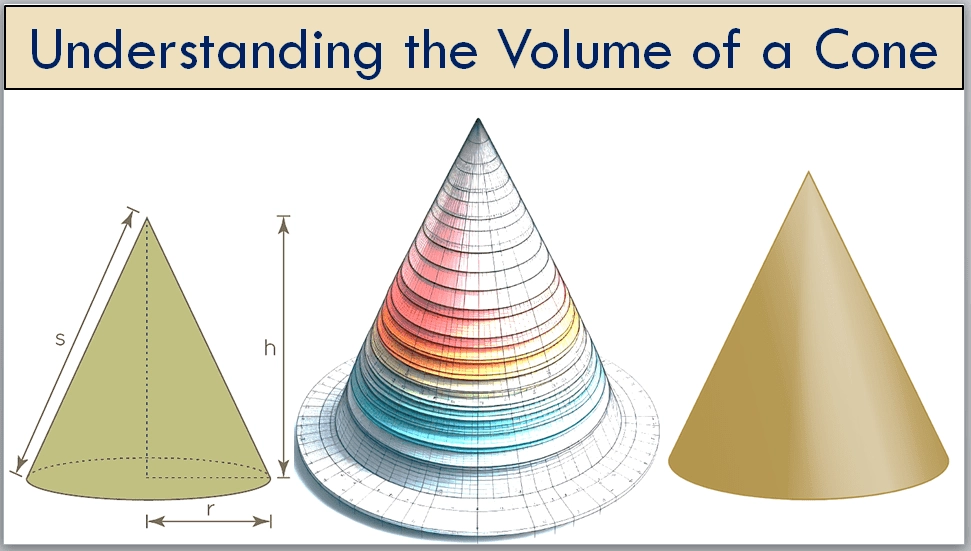
A cone is a three-dimensional geometric shape, also known as a dimensional object, that resembles a pyramid with a circular base. It tapers smoothly from a flat, circular base to a single point called the apex or vertex. Cones come in various sizes and can be found in nature (like pine cones) or manufactured objects (such as traffic cones)

1. The key features that define a cone
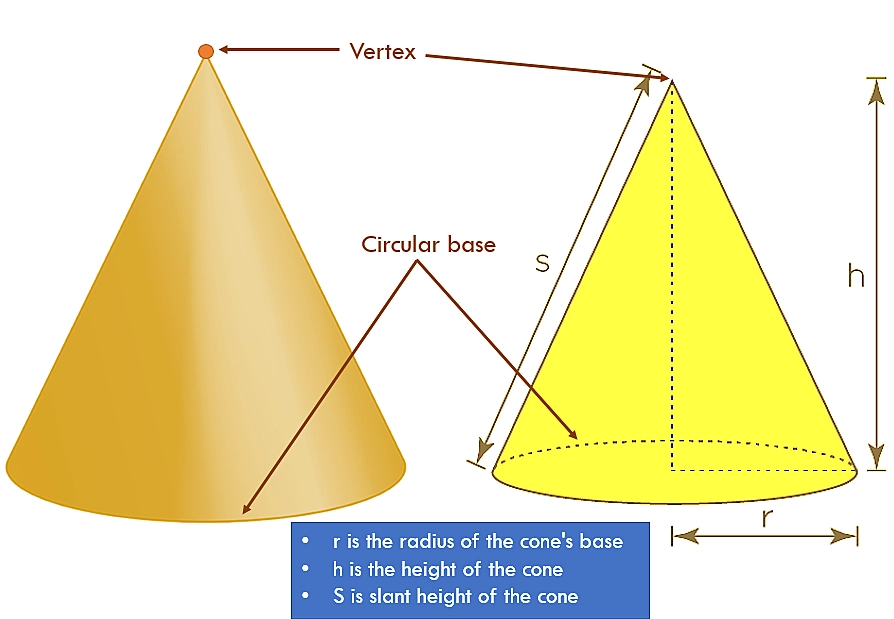
Circular base
The base of a cone is a circle. The radius or diameter of this circle base can vary in size.
Vertex
The topmost point of a cone is called the vertex or apex.
Lateral surface
The curved surface that connects the circular base to the vertex is called the lateral or slant surface. It tapers from the base circumference to the vertex in a slope.
2. Types of the cone There are two types of cones
Right Circular Cone and Oblique Cone
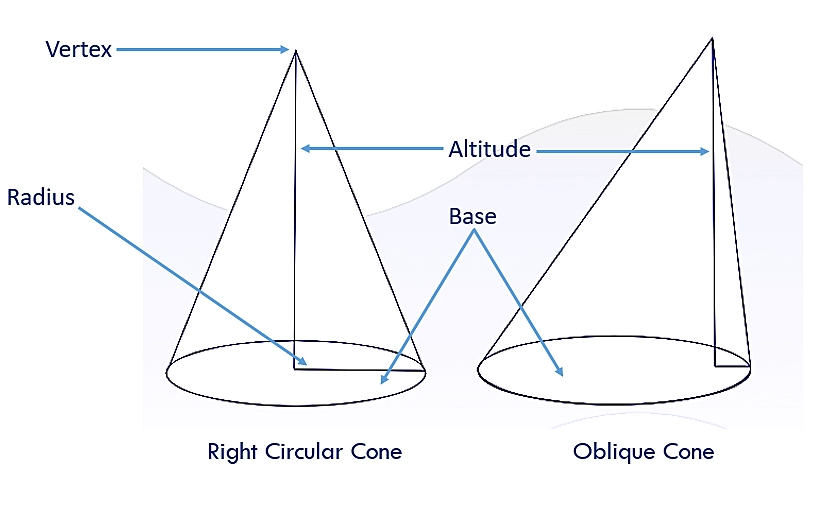
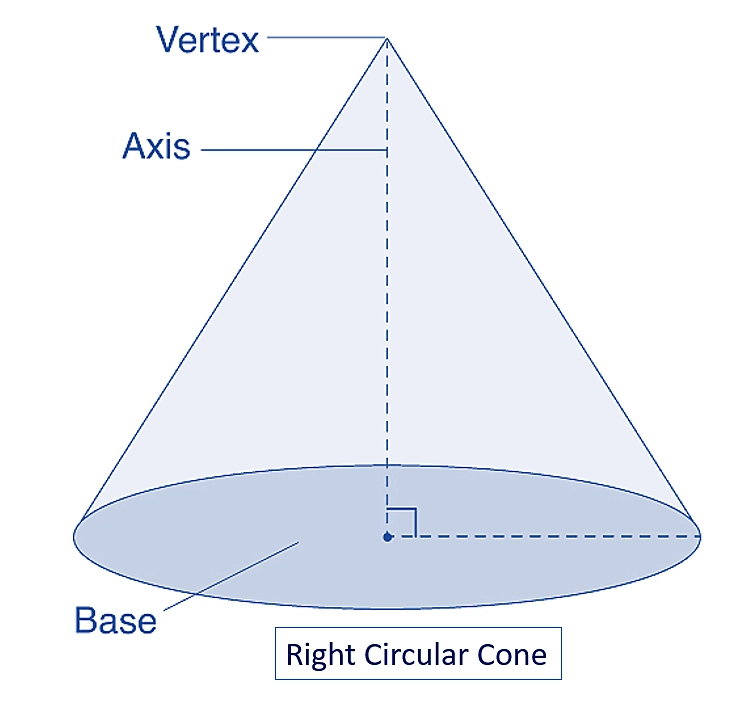
3. Right Circular Cone
A cone which has a circular base and the axis from the vertex of the cone towards the base passes through the center of the circular base. The vertex of the cone lies just above the center of the circular base.
The word “right” is used here because the axis forms a right angle with the base of the cone or is perpendicular to the base. The volume formula for any cone is Volume = 1/3 π r^2 h, where r is the radius of the base of the cone and h is the perpendicular height of the cone.
4. Oblique Cone
A cone that has a circular base but no axis perpendicular to the base is called an oblique cone. The vertex of this cone is not located directly above the center of the circular base.
5. Significance of Cones
Cones are more than just pretty shapes; they are crucial in various scientific and mathematical fields. They have widespread applications in both science and mathematics. In science, they are prevalent in optics, acoustics, and fluid dynamics.
In mathematics, cones are essential in geometry and calculus. They serve as the foundation for understanding three-dimensional shapes and are a vital element in calculus when exploring surfaces and volumes of revolution.

Physics: Rockets and airplanes' aerodynamics often incorporate cones to minimize air resistance and achieve optimal lift.
Engineering: Cones are used in constructing bridges, dams, and other structures due to their inherent stability and strength.
Geometry: Cones are fundamental in studying volume, surface area, and other geometric properties
In physics, cones demonstrate principles of forces, fluids, and more when objects interact with their sloped lateral surface.
Calculus: Understanding cones is essential for calculating integrals and understanding volumes of revolution.
Many objects in everyday life take the basic shape of a cone, like traffic cones, megaphones, candle flames, certain roofs, etc. Understanding cones aids practical applications.

6. Calculating the Volume of a Cone
To calculate the volume of a cone, you should
Measure the height (h) from the center of the circular base to the apex
Measure the radius (r) of the circular base
Plug h and r into the formula and solve
The volume of a cone, or the amount of space it occupies, can be calculated using a simple formula:
The Volume of a Cone V= πr²h
Volume of a Cone = (1/3)πr²h
7. where
V is the volume
π (pi) is a mathematical constant approximately equal to 3.14
r is the radius of the cone's base
h is the height of the cone, measured from the apex to the center of the base
8. Breaking Down the Formula
This formula encapsulates the geometric essence of the cone, emphasizing the contributions of both the base area and the height in determining its volume.
πr²: This part represents the area of the cone's base.
h: This represents the cone's "depth".
(1/3): This is a magic number that accounts for the cone's pointy shape compared to a cylinder with the same base and height.
9. How do you find the height of a cone given its volume and radius?
To find the height (h) of a cone given its volume (V) and radius (r), you can rearrange the formula for the volume of a cone to solve for h The formula gives the volume (V) of a cone:
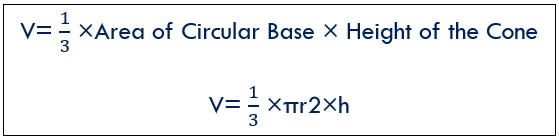
To find h, you can rearrange this formula as follows:

So, if you know the volume (V) and the radius (r), you can substitute these values into the formula to find the height (h) of the cone. The formula is:
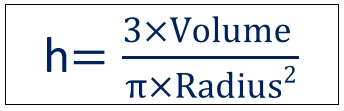
Just plug in the values for the volume and radius, perform the calculations, and you'll find the height of the cone.
10. Examples and Explanations
1. A cone has a base radius of 5 cm and a height of 12 cm.
Calculate its volume.
The volume formula for a cone with height h and base radius r is: Volume = 1/3 π r2 h Let's calculate the volume of this cone using the cone volume formula:
Base radius (r) = 5 cm
Height (h) = 12 cm
The volume of a cone is V = 1/3 π r^2 h
Substituting the values: V = 1/3 x π x (5 cm)^2 x (12 cm) V = 1/3 x 3.14 x (25 cm^2) x (12 cm) V = 1/3 x 3.14 x 300 cm^3 V = 314 cm^3 Therefore, the volume of a cone with a base radius of 5 cm and a height of 12 cm is 314 cm3.
2. Calculate the cone's height if its radius is 5 cm and volume is 100 cubic cm. We can find the height of the cone using the formula for the volume of a cone:
V = (1/3)πr²h
11. where
V is the volume of the cone (100 cubic cm)
π is the mathematical constant pi (approximately 3.14159)
r is the radius of the cone's base (5 cm)
h is the height of the cone (unknown)
Let's rearrange the formula to solve for h:

h = 3V / (πr²) h = 3 x 100 cm³ / (π x 5 cm²)
Calculate the result
h = 3 x 100 cm³ / (3.14159 x 25 cm²) = 3.82 cm Therefore, the height of the cone is approximately
3.82 centimeters.
Fun Facts About Cones
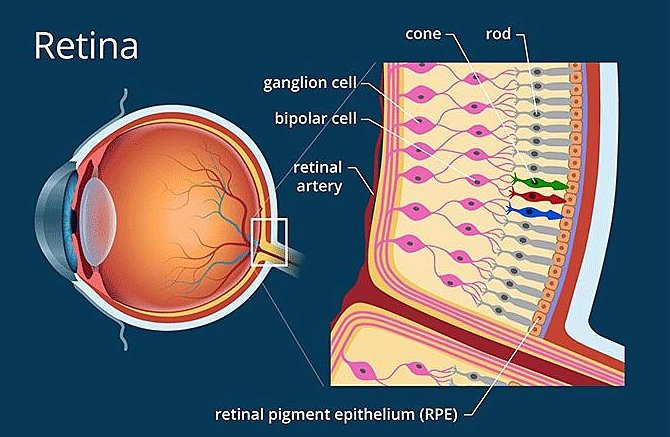
Did you know the human eye has millions of cone cells responsible for color vision? These cone-shaped cells detect different wavelengths of light, allowing us to perceive the rainbow around us.
Ice cream cones were invented 1904 at the St. Louis World Fair to prevent messy hands from waffle cones.
Pineapples, muffins, traffic cones and certain roofs are examples of cones we see everyday.
Traffic cones, with their bright orange glow, are a safety staple worldwide. Their cone shape is easily recognizable and serves as a warning, preventing accidents.
Ancient builders, as seen in the Egyptian pyramids, knew how to create perfectly pointed cones.
The Great Pyramid of Giza in Egypt is an example of a frustum, a cone with its top cut off.
Early study of cones also led to a broader understanding of circles, spheres, and cylinders.
A cone's sloped shape allows fluids, objects, and forces to interact along its surface in valuable ways.
Looking for math instructor? Hire EnthuZiastic Math Experts to master in math no time.
Conclusion
From towering mountains to swirling galaxies, cones are ubiquitous in the natural world. Understanding geometric cones' unique shape, volume, characteristics, and significance allows broader and deeper insights across math, science, architecture, and design.
Observing cones around us, such as ice cream cones or conifer trees, also allows us to appreciate the beauty of geometry in everyday life. From the elegance of their form to their practical applications in various fields, cones offer a fascinating journey through the realms of science and math.
Remember the fascinating world of cones beneath their simple form, and calculate their volume using a cone calculator.FAQs
FAQ’s
1. What is the formula for calculating the volume of a cone, and what do the variables represent?
The formula for calculating the volume of a cone is V = 1/3 π r2 h In this formula, π is a mathematical constant, r is the radius of the cone's base, and h is the height of the cone.
2. In which areas of science are cones commonly used, and how do they play a role in those fields?
Cones find applications in optics, acoustics, and fluid dynamics within the realm of science. They are often used in designing items like loudspeakers, megaphones, and aerodynamic components such as the nose cones of rockets.
3. Provide an example of calculating the volume of a cone with specific values for radius and height.
For instance, if the radius (r) of a cone is 5 units and the height (h) is 8 units, the volume (V) can be calculated using the formula V = 1/3 π (52)(8), resulting in approximately 209.44 cubic units.
4. How do cones contribute to our understanding of geometry and calculus in mathematics?
In mathematics, cones serve as foundational elements in geometry and calculus. They play a crucial role in understanding three-dimensional shapes and are essential in calculus when exploring surfaces and volumes of revolution, enriching our comprehension of mathematical concepts.
5. How does the radius and height of a cone affect its volume?
The volume of a cone is directly proportional to the square of its radius and height. As the radius increases, the volume increases exponentially. Similarly, as the height increases, the volume also increases exponentially





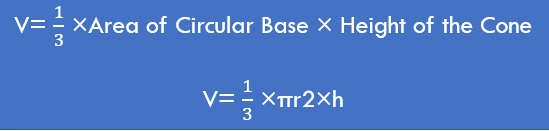
.png)

Comments