Tired of memorizing endless multiplication tables? You’re not alone. For most students, multiplication feels like one of those necessary but boring parts of math especially when numbers start to grow beyond the comfort of single digits. But what if math didn’t have to be a chore? What if there was a way to see how multiplication works instead of just calculating it on paper?
Enter Japanese Multiplication, a fascinating visual method that transforms multiplication into something that looks more like art than arithmetic. By simply drawing lines and counting intersections, this method turns what was once a mechanical process into an intuitive, creative exercise. It’s not only fun but also a powerful way to understand what’s really happening behind the numbers.
What is Japanese Multiplication?
Japanese Multiplication, sometimes referred to as line multiplication or lattice line method, is a visual way to multiply numbers by representing each digit as a set of lines. Instead of relying on rote memorization or traditional algorithms, this approach lets you draw multiplication - literally.
Here’s the concept:
Each digit in a number is represented by a group of parallel lines.
The first number’s lines are drawn diagonally in one direction.
The second number’s lines are drawn diagonally in the opposite direction, creating intersections.
The number of intersection points in different regions corresponds to the hundreds, tens, and ones places of your final answer.
The magic happens when you count those intersections. It’s as if multiplication comes to life before your eyes.
Unlike traditional methods, which often hide the “why” behind steps and carryovers, this method shows multiplication in action. You can actually see how each digit interacts with another digit - helping learners connect logic, visuals, and arithmetic all at once.
How Does It Work? (Step-by-Step Example)
Let’s walk through the steps using a simple example: 12 × 13
Step 1: Draw Lines for the First Number
For 12, draw:
1 line for the tens digit (1)
2 lines for the ones digit (2)
Keep a small space between these two groups.
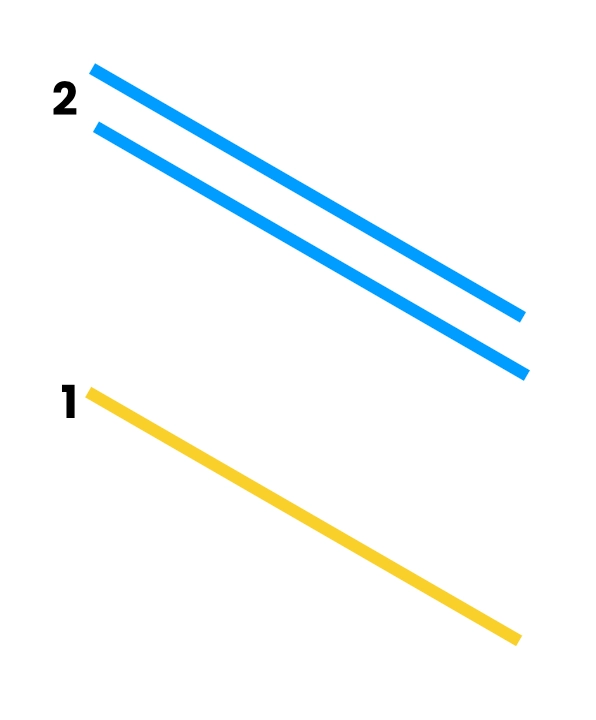
Step 2: Draw Lines for the Second Number
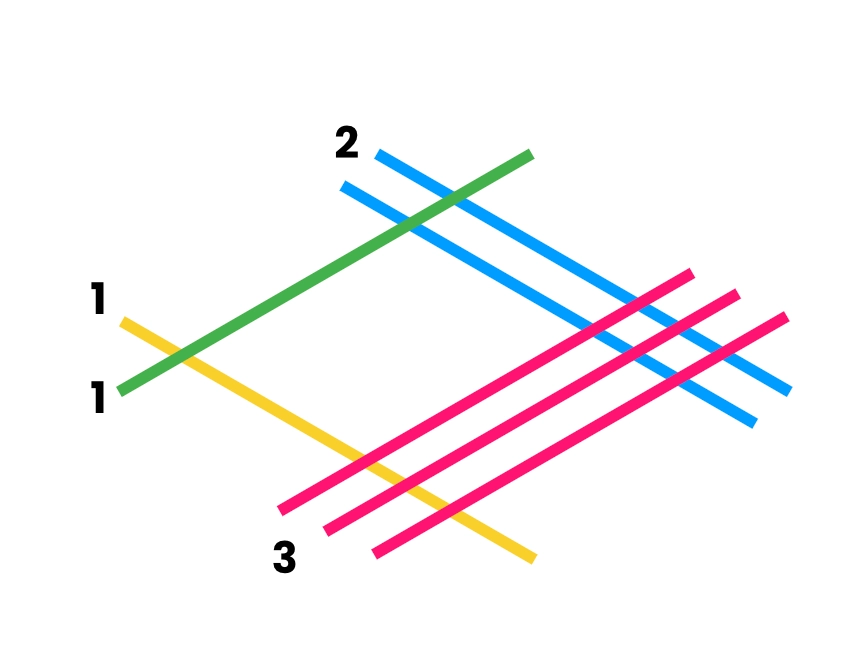
For 13, draw:
1 line for the tens digit (1)
3 lines for the ones digit (3)
Draw these sets of lines perpendicular (or diagonally in the opposite direction) to the first set.
Now your paper looks like a mesh of crisscrossing lines - something between geometry and art.
Step 3: Identify Intersections
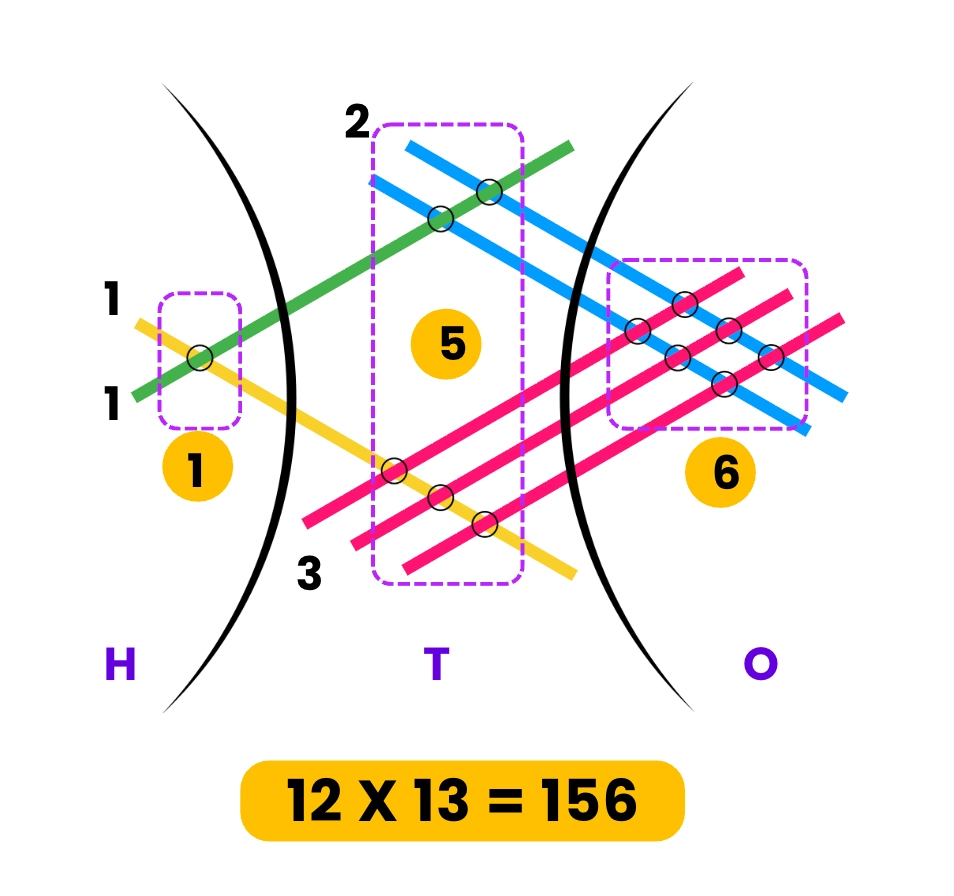
You’ll notice three main areas where the lines intersect:
Top Left: Tens × Tens (hundreds place)
Middle: Tens × Ones and Ones × Tens (tens place)
Bottom Right: Ones × Ones (ones place)

Step 4: Count the Intersections
Let’s count:
Top Left (1×1): 1 intersection → represents 100s
Middle (1×3 and 2×1): 3 + 2 = 5 intersections → represents 10s
Bottom Right (2×3): 6 intersections → represents 1s
Now combine them: 100 + 50 + 6 = 156
Final Answer: ✅ 12 × 13 = 156
You didn’t use a calculator or memorize tables - just lines and logic.

Why Japanese Multiplication Works
Japanese Multiplication isn’t magic, it’s pure math visualized. It’s based on one of the most fundamental arithmetic principles: the distributive property.
(10+2)×(10+3)=(10×10)+(10×3)+(2×10)+(2×3)(10 + 2) × (10 + 3) = (10×10) + (10×3) + (2×10) + (2×3)(10+2)×(10+3)=(10×10)+(10×3)+(2×10)+(2×3)
Each group of intersections visually represents one part of this equation.
The top-left cluster of intersections represents 10×10.
The middle bands represent 10×3 and 2×10.
The bottom-right group represents 2×3.
By counting intersections in each zone, you’re effectively doing what the distributive property does - but with your eyes instead of long written steps.
This visualization makes abstract math feel concrete, which is especially powerful for younger learners or anyone who struggles with mental math.
Strengths of Japanese Multiplication
1. Highly Visual Learning
For visual learners, numbers can sometimes feel abstract. Japanese Multiplication bridges that gap beautifully by showing how quantities interact. The process of drawing lines and counting intersections provides a tactile and visual experience, which enhances comprehension and retention.
2. Encourages Conceptual Understanding
Rather than memorizing procedures, students begin to understand what multiplication truly represents a sum of groups or areas. It helps internalize place value, digit interaction, and the meaning of “carrying over.”
3. Error Reduction
Since every part of the process is visible, errors are easier to catch. If your final sum seems off, you can simply recheck your intersections. The transparency of the process minimizes unnoticed calculation mistakes.
4. Fun and Engaging
There’s no denying it this method feels like play! It transforms multiplication from a dull task into a creative visual activity. Children often describe it as “drawing math,” which makes practice much more enjoyable.
5. Improves Number Sense
Understanding that 23 × 14 is actually (20 + 3)(10 + 4) and seeing that visually builds stronger number sense. This helps not just with multiplication, but also with algebra and problem-solving later on.

Challenges of Japanese Multiplication
Of course, no method is perfect. While Japanese Multiplication is great for understanding and small numbers, it has its limitations:
1. Not Efficient for Large Numbers
Imagine trying to multiply 734 × 568 using this technique — you’d be drawing dozens of lines! It becomes visually cluttered and impractical beyond two-digit numbers.
2. Time-Consuming
It’s slower compared to traditional long multiplication or mental math. That’s why it’s best suited as a learning tool rather than a calculation shortcut.
3. Requires Neatness and Precision
A slight misalignment or skipping a line can change your answer. It’s important to draw lines carefully and keep spaces consistent for clarity.
4. Not Always Scalable
The visual grid works best when numbers are neat and small. Once you get to decimals, fractions, or three-digit multiplications, managing intersections can be tricky.
Real-Life Scenarios Where It Helps
Even with its limitations, Japanese Multiplication is incredibly useful in several settings:
1. Teaching Kids Multiplication
It’s an excellent classroom activity for teachers introducing multiplication concepts. Instead of jumping directly into memorization, children can first see how multiplication works.
2. Visualizing Math Concepts
For visual learners, seeing math in action improves comprehension and memory retention. It can also help neurodivergent students or those who struggle with traditional learning styles.
3. Brain Training and Pattern Recognition
This technique enhances pattern recognition and spatial reasoning — skills useful not only in math but also in coding, design, and logic-based problem solving.
4. Homeschooling or Tutoring
Parents teaching math at home can use this method to make lessons interactive. It encourages curiosity and gives children confidence in understanding numbers visually.
5. Cross-Cultural Math Learning
It’s also a great way to explore how different cultures approach mathematics, introducing students to the diversity of problem-solving methods used worldwide.
Evidence and Research Support
Educational research consistently supports visual learning in math. Studies show that:
Students who use visual representations develop better number sense and deeper conceptual understanding.
Visual methods boost engagement, helping children retain information longer.
Hands-on and drawing-based techniques promote creativity and confidence in solving problems.
For instance, researchers in math pedagogy have observed that when learners combine visual and symbolic forms, their ability to solve complex problems improves significantly. The Japanese Multiplication method, therefore, fits perfectly into modern learning models that emphasize understanding over memorization.
Tips for Mastering Japanese Multiplication
Start Simple – Begin with single-digit examples like 3×4 or 5×6 before moving to two-digit numbers.
Use Graph Paper – It helps maintain alignment and makes counting intersections easier.
Group Carefully – Always separate intersections into hundreds, tens, and ones before adding.
Double-Check Intersections – Count twice to avoid minor errors.
Practice Regularly – The more you practice, the faster you’ll become at visual grouping.
Involve Creativity – Use colored pens or markers to represent different digits or groups. This enhances understanding and makes the process more engaging.
Explain While You Draw – If you’re teaching someone, narrate each step aloud. Teaching reinforces understanding.
Gradually Increase Complexity – Once you’re comfortable with two-digit numbers, try small three-digit ones or simple decimals.
Conclusion
Japanese Multiplication is more than just a math trick it’s an eye-opening way to experience numbers. By merging visualization, creativity, and arithmetic, it transforms multiplication into something you can literally see and understand.
While it may not replace the speed of traditional methods, it excels in building conceptual clarity, pattern recognition, and number confidence. Whether you’re a student exploring math, a teacher searching for new teaching tools, or a parent helping your child overcome math anxiety, this method offers a refreshing, joyful approach to learning.
At its heart, math isn’t about memorizing numbers it’s about understanding relationships. And Japanese Multiplication reminds us that sometimes, the best way to understand those relationships is to draw them.
FAQs
1. What exactly is Japanese Multiplication?
Japanese Multiplication is a visual method of multiplying numbers using lines and intersections. Each digit of a number is represented by parallel lines, and counting the intersection points gives the product.
2. Why is it called Japanese Multiplication?
Although it’s widely known by this name, the method is not strictly Japanese. Variations of it have appeared in several Asian cultures, including Japan, China, and India. The name became popular through viral educational videos online.
3. Can Japanese Multiplication be used for all numbers?
Technically yes, but it becomes impractical for very large numbers because the number of lines increases dramatically, making it hard to count intersections accurately.
4. Does Japanese Multiplication help children understand math better?
Yes! It’s especially useful for visual learners as it helps them understand the logic behind multiplication rather than just memorizing tables.
5. Can this method be used for decimals or fractions?
Yes, but it requires extra care in drawing lines and placing decimal points correctly. It’s best to master whole numbers first.
6. Is Japanese Multiplication faster than traditional multiplication?
Not necessarily. It’s slower for large or complex numbers, but faster for understanding basic multiplication concepts visually.
7. What skills does Japanese Multiplication help develop?
It enhances visual-spatial reasoning, pattern recognition, number sense, and logical thinking, all key skills for problem-solving.
8. Can teachers use this in classrooms?
Absolutely! It’s a great teaching tool to make math lessons more interactive and engaging. It also helps students grasp place value and multiplication principles clearly.
9. Is this method used in modern Japanese schools?
Not officially. Japanese schools mainly use standard arithmetic methods, but this technique is sometimes taught as a fun alternative or enrichment activity.
10. What materials do I need to try Japanese Multiplication?
All you need is paper, a pencil or pen, and patience! Graph paper or color markers can make it easier to keep lines aligned and intersections clear.






Comments